1.5. Числа Фибоначчи - математическая основа теории волн
Как признавал сам Эллиот в своей работе "Законы природы", математической основой теории стала последовательность чисел, которую открыл (или, чтобы быть точнее, вновь открыл) Фибоначчи в XIII веке. В его честь открытую им последовательность стали называть "числами Фибоначчи".
Фибоначчи в свое время опубликовал три большие работы, самая знаменитая из которых называется "Liber Abaci". Благодаря этой книге Европа узнала индо-арабскую систему чисел, которая позднее вытеснила традиционные для того времени римские числа. Работы Фибоначчи имели огромное значение для последующего развития математики, физики, астрономии и техники. В "Liber Abaci" Фибоначчи приводит свою последовательность чисел как решение математической задачи - нахождение формулы размножения кроликов. Числовая последовательность такова: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 (далее до бесконечности). Последовательность Фибоначчи имеет весьма любопытные особенности, не последняя из которых - почти постоянная взаимосвязь между числами.
Сумма любых двух соседних чисел равна следующему числу в последовательности. Например: 3 + 5 = 8; 5 + 8 = 13 и т.д.
Отношение любого числа последовательности к следующему приближается к 0,618 (после первых четырех чисел). Например: 1: 1 = 1; 1: 2 = 0,5; 2: 3 = 0,67; 3: 5 = 0,6; 5: 8 = 0,625; 8: 13 = 0,615; 13: 21 = 0,619 и т.д. Обратите внимание, как значение соотношений колеблется вокруг величины 0,618, причем размах флуктуаций постепенно сужается; а также на величины: 1,00; 0,5; 0,67.
Отношение любого числа к предыдущему приблизительно равно 1,618 (величина обратная 0,618). Например: 13: 8 = 1,625; 21: 13 = 1,615; 34: 21 = 1,619. Чем выше числа, тем более они приближаются к величине 0,618 и 1,618.
Отношение любого числа к следующему за ним через одно приближается к 0,382, а к предшествующему через одно - 2,618. Например: 13: 34 = 0,382; 34: 13 = 2,615.
Последовательность Фибоначчи содержит и другие любопытные соотношения, или коэффициент, но те, которые мы только что привели - самые важные и известные. Как мы уже подчеркивали выше, на самом деле Фибоначчи не является первооткрывателем своей последовательности. Дело в том, что коэффициент 1,618 или 0,618 был известен еще древнегреческим и древнеегипетским математикам, которые называли его "золотым коэффициентом" или "золотым сечением". Его следы мы находим в музыке, изобразительном искусстве, архитектуре и биологии. Греки использовали принцип "золотого сечения" при строительстве Парфенона, египтяне - Великой пирамиды в Гизе. Свойства "золотого коэффициента" были хорошо известны Пифагору, Платону и Леонардо да Винчи.
Пропорции чисел Фибоначчи дают ориентиры не только возможных уровней отката, но и указывают возможную величину хода в случае продолжения тенденции. Если после хода рынок откатывается, а затем продолжает ход в том же направлении, то в типичном случае величина продолженного хода может составить 1.618.
Заключение
Полный цикл "бычьего" рынка состоит из 8 волн: 5 волн роста, за которыми следуют 3 волны падения.
Тенденция подразделяется на 5 волн в направлении следующей в иерархии, более продолжительной тенденции.
Коррекция всегда состоит из трех волн.
Простые коррекции бывают двух типов: зигзаги 5-3-5 и плоские волны 3-3-5.
Треугольники, как правило, образуются на четвертых волнах (эта модель всегда предшествует последней волне). Треугольник может также быть корректирующей волной В.
Любая волна является частью более длинной и подразделяется на более короткие.
Иногда одна из импульсных волн растягивается. Остальные две должны оставаться равными по времени и протяженности.
Математической основой теории волн Эллиота является последовательность Фибоначчи.
Количество волн, образующих тенденцию, совпадает с числами Фибоначчи.
Коэффициенты Фибоначчи и основанные на них отношения длины коррекции используются для определения ценовых ориентиров. Отношение длины коррекции к предыдущему движению рынка часто равняется 62%, 50% и 38% (Рис 23).
Правило чередования предупреждает, что не следует ждать одинакового проявления ценовой динамики два раза подряд.
"Бычьи" рынки не должны опускаться ниже основания предыдущей четвертой волны.
Волна 4 не должна перехлестываться с волной 1
Основными аспектами теории волн Элиота являются (в порядке значимости): форма волны, соотношение волн и время.
Кроме того, в самом общем виде система приложения чисел Фибоначчи к рынку FOREX работает следующим образом.
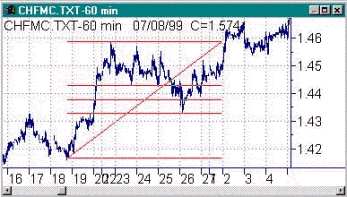
Рис. 23
Методика прогностических расчетов строится на том, что численное соотношение значений "движение - откат" должно давать коэффициенты "золотого сечения", то есть:
- 1,618; 2,618; 4,236 (при движении);
- 0,618;' 0,382; 0,236 (при откате);
Эти численные значения и представляют собой те важные уровни, которые рынок "вспоминает" по ходу изменения цен. Именно на них ориентируется трейдер в своей игре.
Наиболее простое употребление числа Фибоначчи находят при расчете уровня отката (retracement) или отскока (rebound). Так как цены не могут непрерывно расти или падать продолжительное время, после каждого их изменения существует той или иной величины откат в противоположную сторону. Особенно ярко это явление видно после сильного и продолжительного движения. При этом откат 33% наиболее вероятен, а откат 66% наименее вероятен (рис. 24).
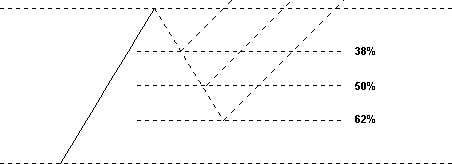
Рис. 24
Использование последовательности Фибоначчи позволяет увеличить наиболее вероятную нижнюю границу с 33% до 38,2% (число Фибоначчи 0,382) и в то же время уменьшить наименее вероятную дальнюю границу с 66% до 61,8% (число Фибоначчи 0,618). Достижение уровня в 38,2% происходит чрезвычайно часто, что обусловлено огромной популярностью теории Эллиота. Действительно, поскольку большинство участников рынка ожидает именно такой откат, именно он и происходит.
Расчет уровней откатов и отскоков - достаточно простое занятие, что делает этот анализ привлекательным. Кроме того, откаты и отскоки действуют как на главных трендах, так и на вторичных и краткосрочных. Таким образом, их можно наблюдать на недельных и часовых графиках.
|

